My research interests are in the area of networked, large-scale, and dynamic systems, such as power grids, cooperative multi-agent networks, and complex biological systems. My main thrust is on security, reliability, and trust management in cyber-physical systems, with an emphasis on distributed control and estimation of large-scale systems. A second research direction is in network science, and particularly in the intersection between control theory and network neuro- science. A third interest is in mobile robotics, environmental patrolling, and persistent surveillance, with an emphasis on combinatorial optimization, complexity theory, and network algorithms. Below is a description of some selected projects.
Cluster Synchronization in Networks of Oscillators
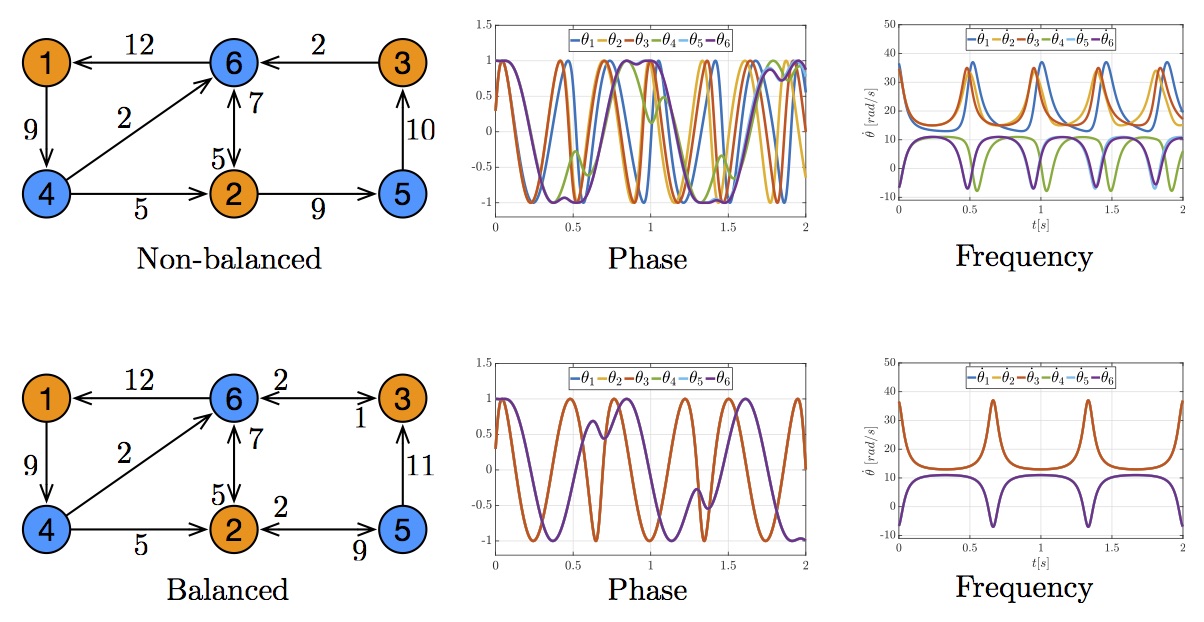
Synchronization of coupled oscillators is
everywhere in nature and in several man-made systems. While some
systems require complete synchronization among all the parts to
function properly, others rely on cluster or partial synchronization,
where subsets of nodes exhibit coherent behaviors that remain
independent from the evolution of other oscillators in the
network. For example, while partial synchronization patterns have been
observed in healthy individuals, complete synchronization in neural
systems is associated with degenerative diseases including Parkinson's
and Huntington's diseases, and epilepsy. Cluster synchronization has
received attention only recently, and several fundamental questions
remain unanswered, including the characterization of the network
features enabling the formation of a desired pattern, and the
development of control mechanisms to enforce the emergence of
clusters.
We have studied networks of heterogeneous Kuramoto
oscillators, and have characterized intrinsic and topological
conditions that ensure the formation of desired clusters of
oscillators. Although Kuramoto networks exhibit nonlinear dynamics, we
adopt tools from linear algebra and graph theory to characterize
network conditions enabling the formation of a given synchronization
pattern. Further, we design a control mechanism to perturb (a subset
of) the network weights so as to enforce or prevent desired
synchronization patterns. For more details see, for instance, our
works Synchronization
Patterns in Networks of Kuramoto Oscillators: A Geometric Approach for
Analysis and Control, Bode meets
Kuramoto: Synchronized Clusters in Oscillatory Networks, and Cluster
Synchronization in Networks of Kuramoto Oscillators.
Analysis and Control of Structural Brain Networks
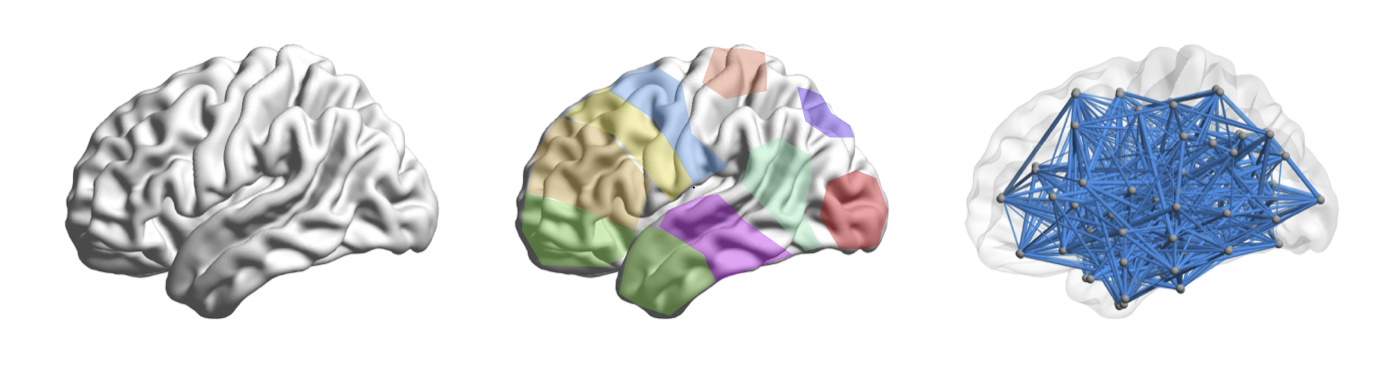
Cognitive function is driven by dynamic
interactions between large-scale neural circuits or networks, enabling
behaviour. However, fundamental principles constraining these dynamic
network processes have remained elusive. Here we use tools from
control and network theories to offer a mechanistic explanation for
how the brain moves between cognitive states drawn from the network
organization of white matter microstructure. Our results suggest that
densely connected areas, particularly in the default mode system,
facilitate the movement of the brain to many easily reachable
states. Weakly connected areas, particularly in cognitive control
systems, facilitate the movement of the brain to difficult-to-reach
states. Areas located on the boundary between network communities,
particularly in attentional control systems, facilitate the
integration or segregation of diverse cognitive systems. Our results
suggest that structural network differences between cognitive circuits
dictate their distinct roles in controlling trajectories of brain
network function. For more details see, for instance, our works Controllability
of structural brain networks, Optimally controlling the human
connectome: the role of network
topology, Stimulation-Based
Control of Dynamic Brain Networks, and Autaptic Connections Shift
Network Excitability and Bursting. Distributed systems and networks have
permeated modern society in many domains including energy production,
health care, and telecommunications. The integration of cyber
technologies with physical processes increases system efficiency but,
at the same time, it introduces vulnerabilities that undermine the
reliability of critical infrastructures -- an infamous example is the
case of the Maroochy water breach. In contrast with legacy control
system, cyber-physical systems are prone to failures and coordinated
attacks against their physical infrastructure, as well as cyber
attacks against their data management and communication
layer. Attackers can now compromise physical processes by exploiting
cyber vulnerabilities, and appropriate cyber-physical protections are
needed -- see the SQL Slammer worm against the David-Besse nuclear
plant, and the Stuxnet worm against the Iranian nuclear
facilities. Cyber-physical security is a multidisciplinary field
involving Control Theory, Game Theory, Computer Security, and
Optimization, and it is attracting interest from several scientific
societies. Networks accomplish complex behaviors
via local interactions of simpler units. The electrical power grid,
mass transportation systems, and cellular networks are instances of
modern technological networks, while metabolic and brain networks are
biological examples. The ability to control and reconfigure complex
networks via external controls is fundamental to guarantee a reliable
and efficient network functionality. Despite important advances in the
theory of control of dynamical systems, several questions regarding
the control of complex networks are largely unexplored. Coordinated teams of autonomous agents
can efficiently complete tasks requiring repetitive execution, such as
monitoring oil spills, detecting forest fires, tracking border
changes, and surveilling an environment. Surveillance of an
environment requires that the robots persistently travel around the
area, and one of the main challenges consists in scheduling the robots
trajectories as to optimize a certain performance criteria. We
consider two different class of robots, namely mobile robots and PTZ
cameras. For the case of mobile robots, we model the environment as a
robotic roadmap, and we consider time-based performance criteria, such
as the longest time gap between any two visits of the same region
(refresh time), and the longest time to propagate a message to all
robots (latency). We formulate deterministic and stochastic
surveillance problems, and we derive centralized and distributed
surveillance strategies with performance guarantees. For the case of
PTZ cameras, we study the interplay between cameras and smart evaders,
and we develop centralized and distributed algorithms for cameras
coordination and detection. For more details see, for instance, our works On
Cooperative Patrolling: Optimal Trajectories, Complexity Analysis and
Approximation Algorithms, Cooperative
Patrolling via Weighted Tours: Performance Analysis and Distributed
Algorithms, Stochastic
Surveillance Strategies for Spatial Quickest Detection, and Camera Network Coordination for Intruder Detection. Sensor and actuator networks have
recently attracted interest from different research communities., and
classic computation, control, and estimation problems have been
reformulated to conform the distributed nature of these networked
systems. An important example is the consensus problem, where members
of a network aim to agree on a parameter of interest via distributed
computation. Consensus algorithms have applicability in many domains,
including robotics, estimation, and parallel computation.
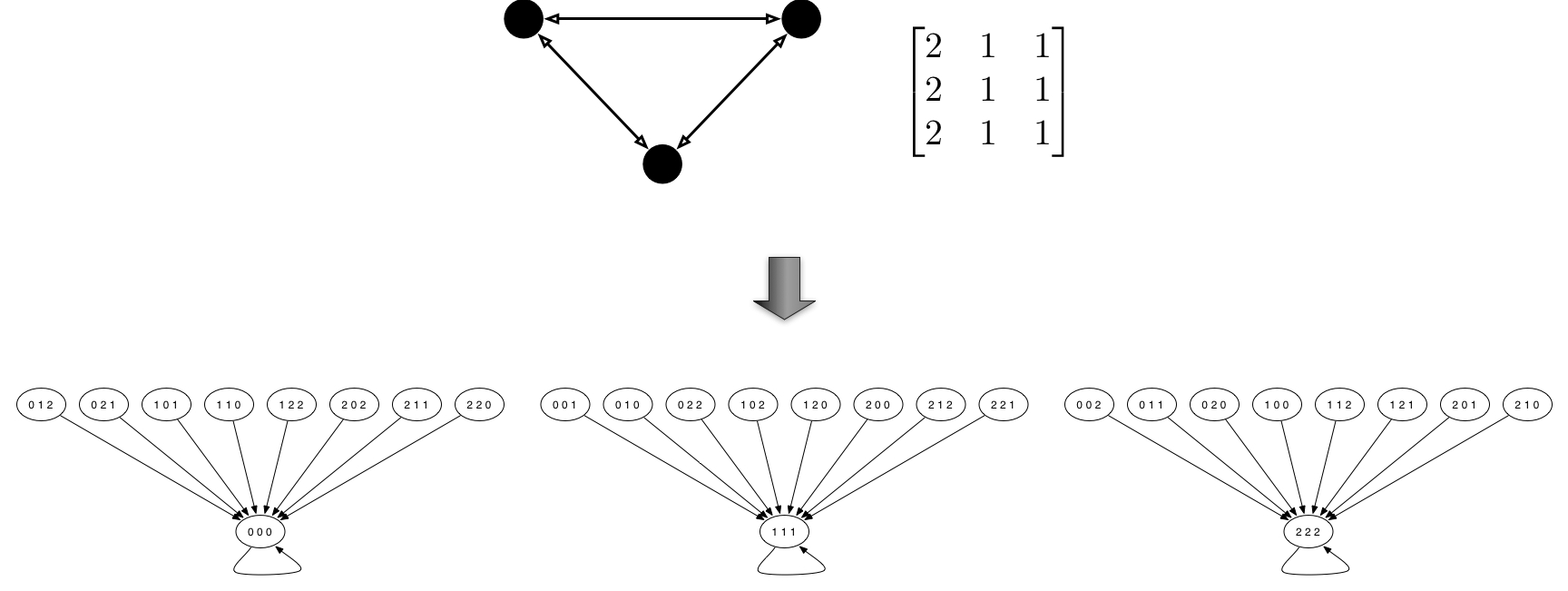
In this work we focus on the consensus problem for networks of agents
with limited memory, computation, and communication capabilities. We
assume that agents are capable of storing, processing, and
transmitting exclusively elements from a finite and pre-specified
alphabet. We model this situation with the formalism of finite fields,
where the alphabet consists of a set of integers, and operations are
performed according to modular arithmetic. We study linear consensus
networks over finite fields where, at each time instant, each agent
updates its state as a weighted combination over a finite field of its
own value and those received from its neighbors. Besides consensus in
capacity and memory constrained networks, our finite-field consensus
method is applicable to problems in cooperative control, networked
systems, and network coding, such as averaging, load balancing, and
pose estimation from relative measurements. Additionally, the use of a
finite alphabet for computation and communication makes our consensus
method easily implementable and resilient to communication noise. For
more details see, for instance, our work Consensus
Networks over Finite Fields. State estimation is needed to maintain
a system in a secure operating condition. For high-dimensional and
spatially distributed systems, centralized methods cannot be used to
solve estimation, control, and fault detection problems, and new
decentralized techniques need to be developed. One possibility is to
deploy monitors in different geographical locations, each one
responsible for a subpart of the whole system. Monitors have local
information about the system topology and state, and implement local
estimation and control schemes together with an information exchange
mechanisms to recover the performance of a centralized scheme. We
propose distributed and scalable algorithms with finite convergence
time for state estimation in large-scale systems. The proposed
monitors (i) require local system knowledge and computation, and
communication among neighboring control centers, (ii) tolerate system
and measurement noise and modeling uncertainties, and (iii) are robust
against a fairly general class of attacks. Finally, our analysis
reveals elegant connections between state estimation, decentralized
control theory, and parallel computation methods. For more details see, for instance,
our works Distributed
Estimation via Iterative Projections with Application to Power Network
Monitoring and Continuous-Time
Distributed Observers with Discrete Communication.Security of Cyber-Physical Systems and Critical
Infrastructures
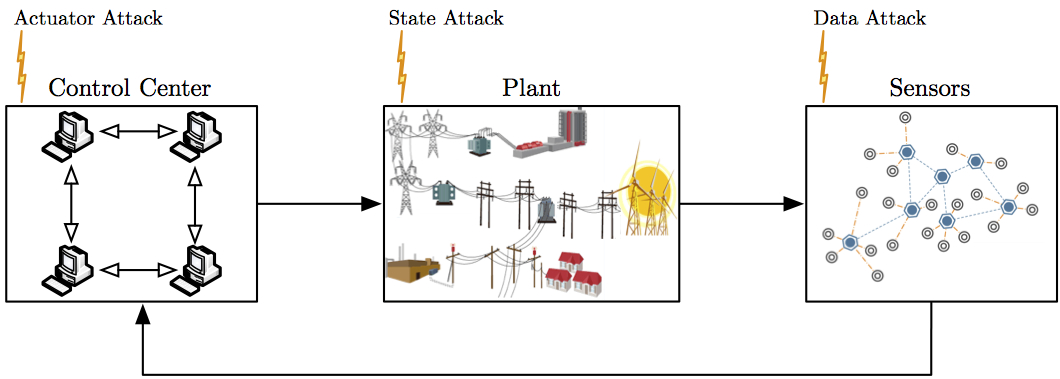
We contribute to cyber-physical security by (i)
proposing a mathematical framework for cyber-physical systems,
malicious attackers, and security monitors, (ii) establishing a
detailed link between security and the fault detection and
identification literature, (iii) characterizing fundamental monitoring
limitations from system-theoretic and graph-theoretic perspectives,
(iv) designing centralized and distributed attack detection and
identification monitors, and (v) providing insight into the design of
coordinated attacks amenable to simple implementation. For more
details see, for instance, our works Consensus
Computation in Unreliable Networks: A System Theoretic Approach,
Attack
Detection and Identification in Cyber-Physical Systems, and Data-injection
attacks in stochastic control systems: Detectability and performance
tradeoffs.Controllability and Observability of Complex Networks
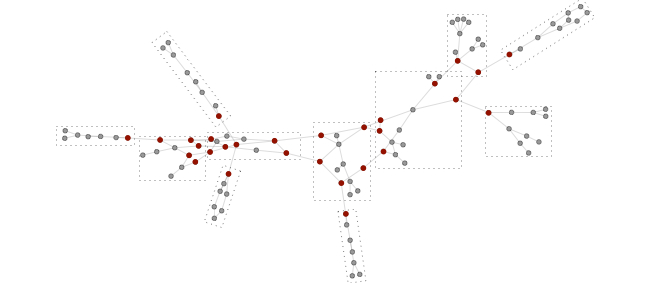
The
problem of controlling complex networks consists of the selection of a
set of control nodes, and the design of a distributed control law to
steer the network to a target state. We study the problem of
controlling complex networks from an energy perspective. Inspired by
classic controllability notions for dynamical systems, we define the
energy to control a network as the worst-case energy of the control
input to reach a target state. By combining this controllability
notion with graph theory, we characterize tradeoffs between the energy
to control a given network and the number of control nodes, and we
develop a distributed control strategy with performance guarantees for
complex networks. For more details see, for instance, our works Controllability
Metrics, Limitations and Algorithms for Complex Networks, The
Observability Radius of Networks, and The Role of
Diameter in the Controllability of Complex Networks.Robotic Patrolling and Surveillance
Networks over Finite-Fields
Distributed Estimation and Control over Networks